Tree
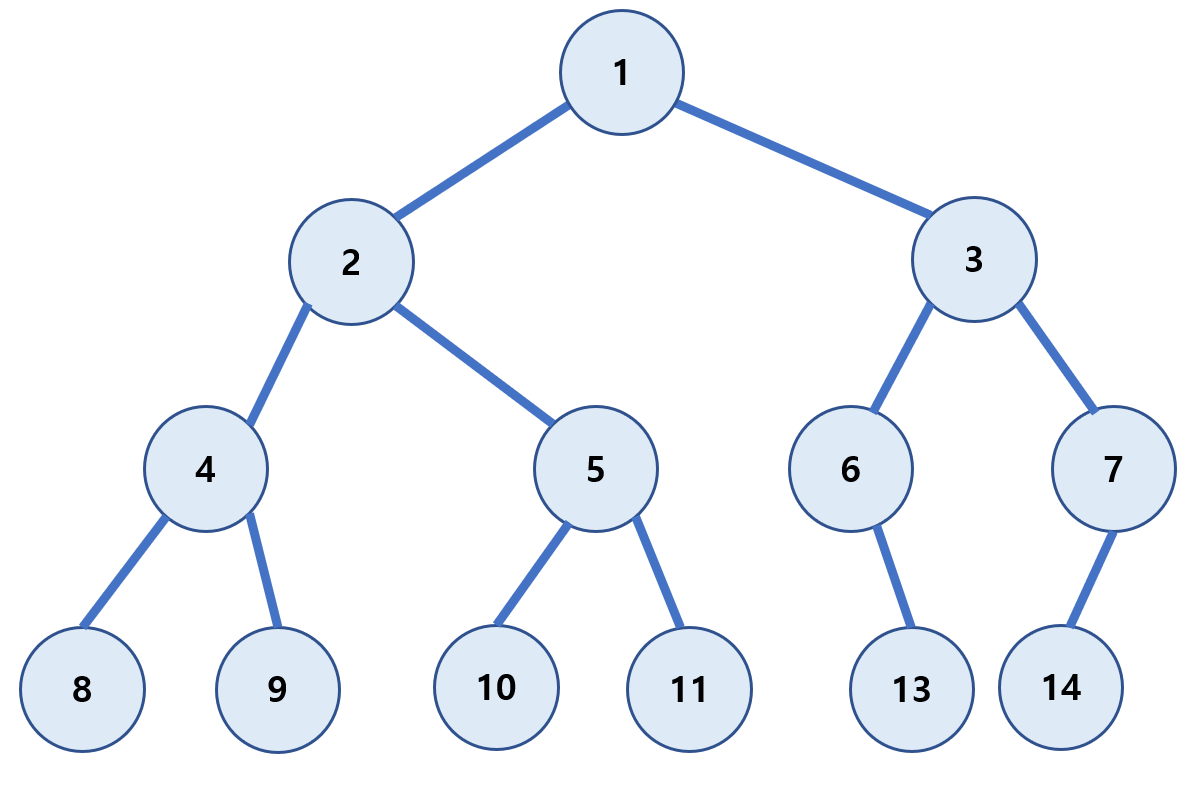
트리는 값을 가진 노드(Node)와 이 노드들을 연결해주는 간선(Edge)으로 이루어져있다.
그림 상 데이터 1을 가진 노드가 루트(Root) 노드다.
모든 노드들은 0개 이상의 자식(Child) 노드를 갖고 있으며 보통 부모-자식 관계로 부른다.
트리에는 사이클이 존재할 수 없다.
💬 사이클?
시작 노드에서 출발해 다른 노드를 거쳐 다시 시작 노드로 돌아올 수 있다면 사이클이 존재한다고 한다.
부모 노드(parent node): 자기 자신(노드)과 연결 된 노드 중 자신보다 높은 노드를 의미 (ex.5의 부모노드 :2)자식 노드(child node): 자기 자신(노드)과 연결 된 노드 중 자신보다 낮은 노드를 의미 (ex.3의 자식노드 :6,7)루트 노드 (root node): 일명 뿌리 노드라고 하며 루트 노드는 하나의 트리에선 하나밖에 존재하지 않고, 부모노드가 없다.
위에선1이 뿌리노드다.단말 노드(leaf node): 리프 노드라고도 불리며 자식 노드가 없는 노드를 의미한다. 위 이미지에서8,9,10,11,13,14노드가 단말노드다.형제 노드(sibling node): 부모가 같은 노드를 말한다. (ex.4,5는 모두 부모노드가2이므로4,5는 형제노드다.)깊이(depth): 특정 노드에 도달하기 위해 거쳐가야 하는 ‘간선의 개수’를 의미 (ex.5의 깊이 :1→2→5이므로 깊이는 2가 됨)레벨(level): 특정 깊이에 있는 노드들의 집합을 말하며, 구현하는 사람에 따라0또는1부터 시작한다.
→1노드를 0 레벨이라 하고2와3의 노드 레벨을 1 레벨이라고 할 수도 있고1노드를 1레벨이라고 하면2와3노드는 2레벨이 된다.차수(degree): 특정 노드가 하위(자식) 노드와 연결 된 개수 (ex.4의 차수 = 2 {8,9} )높이 : 트리의 높이는 루트 노드부터 리프 노드까지 거리 중 가장 긴 거리를 의미하며 위의 트리 높이는 3이다.
🐣 V - 1 = E : 간선 수 = 노드 수 - 1
트리 순회 방식
🐣 root를 기준으로 root가 앞에 있으면 전위, 뒤에 있으면 후위 중간에 있으면 중위로 알면 쉽다.
전위 순회(pre-order)
각 루트(Root)를 순차적으로 먼저 방문하는 방식이다.
(Root → 왼쪽 자식 → 오른쪽 자식)
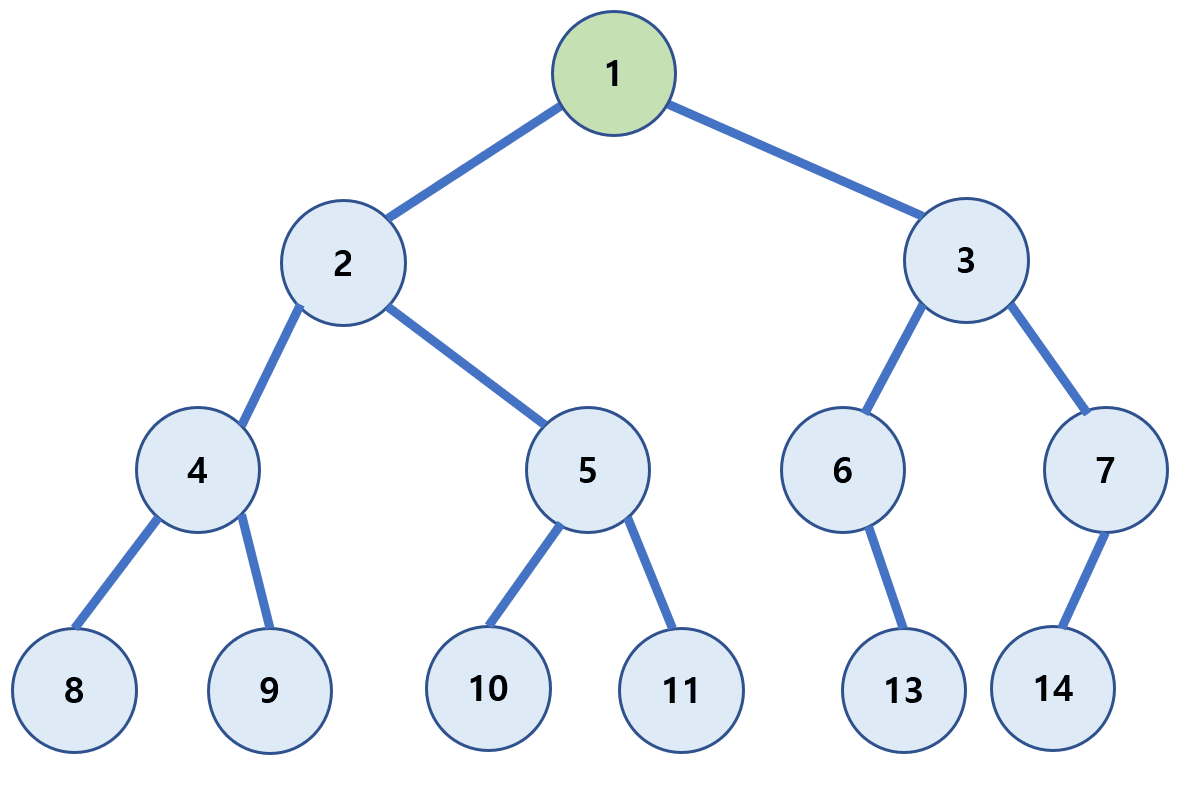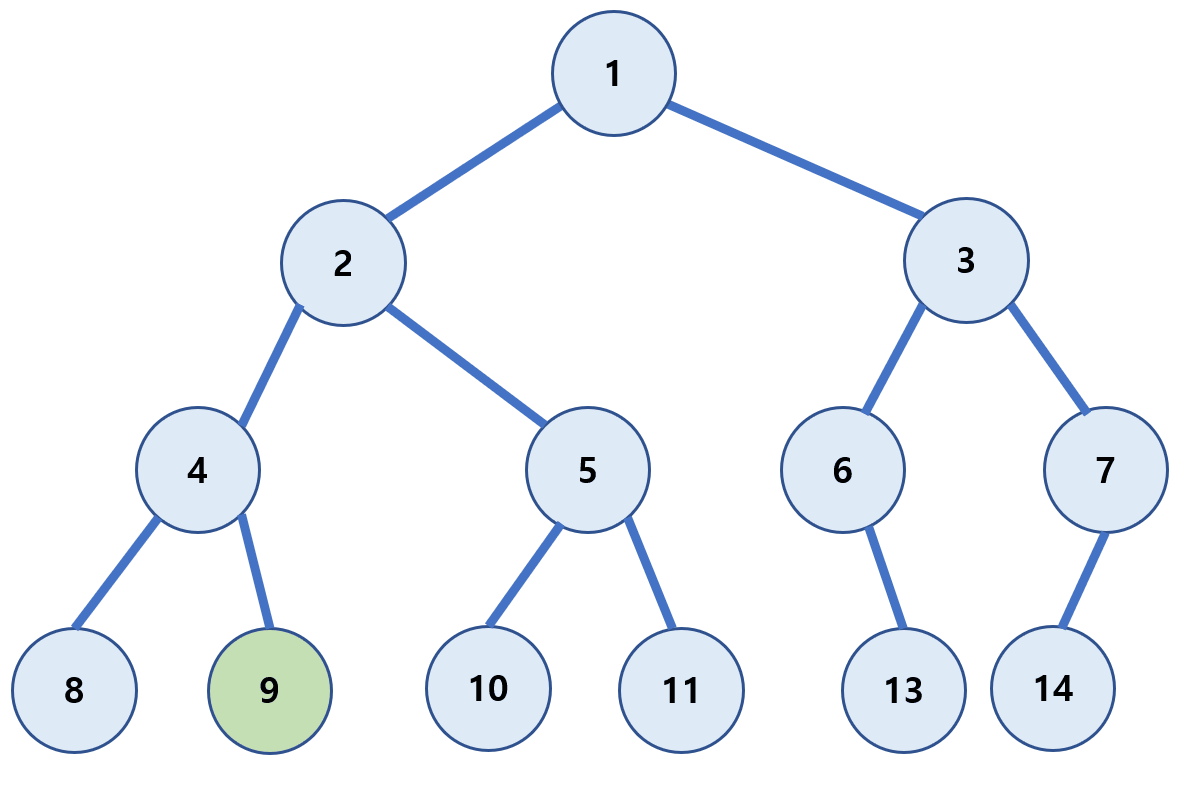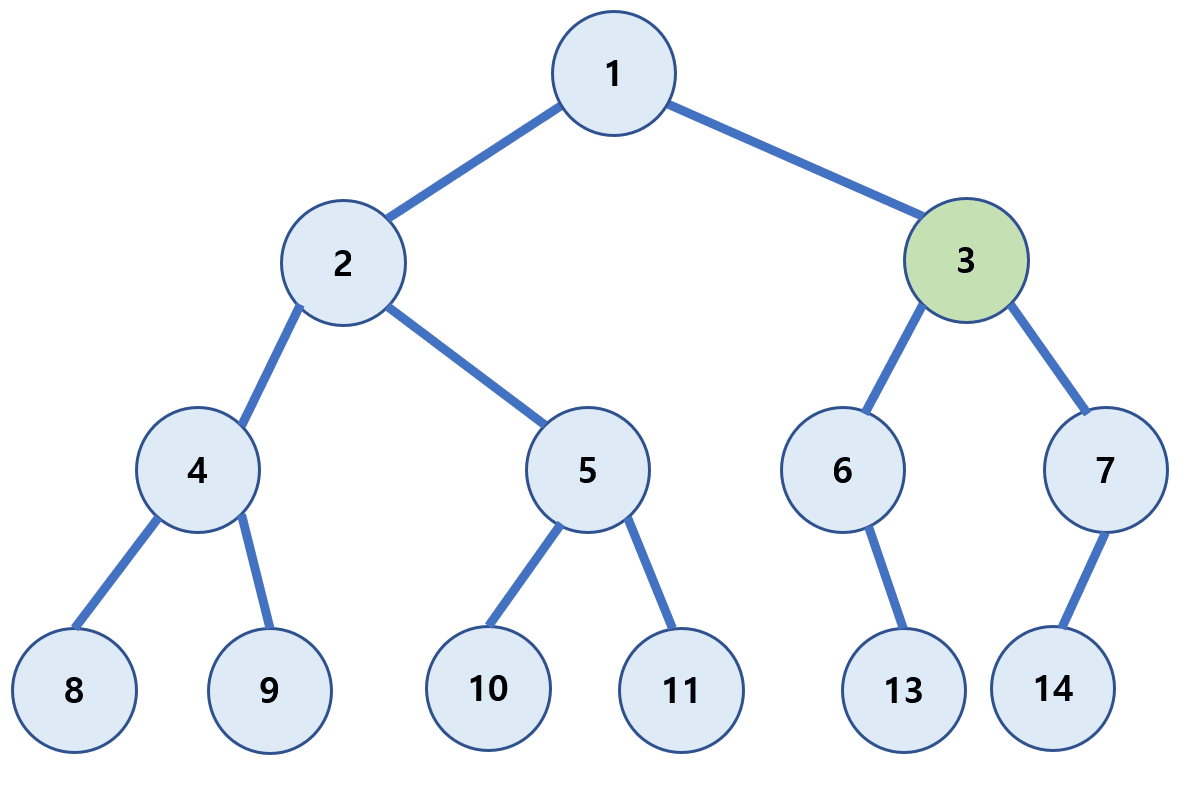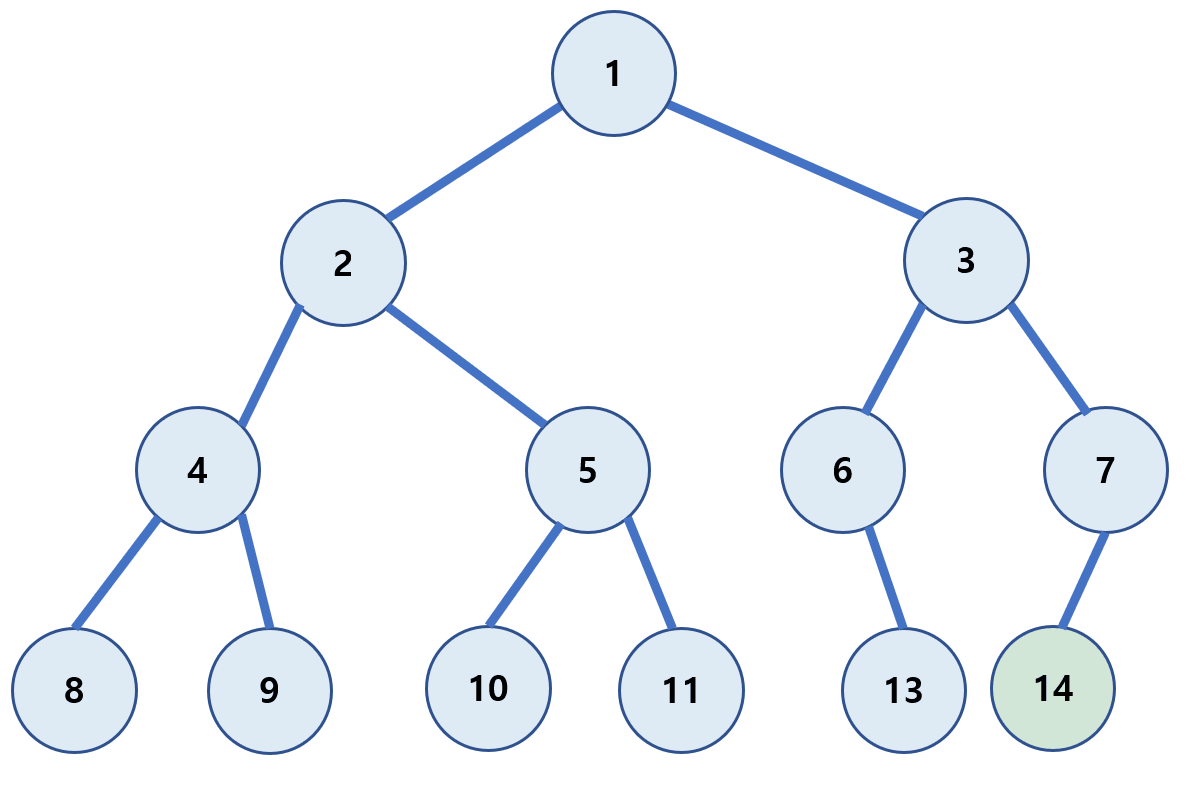
1 → 2 → 4 → 8 → 9 → 5 → 10 → 11 → 3 → 6 → 13 → 7 → 14
중위 순회(in-order)
왼쪽 하위 트리를 방문 후 루트(Root)를 방문하는 방식이다.
(왼쪽 자식 → Root → 오른쪽 자식)
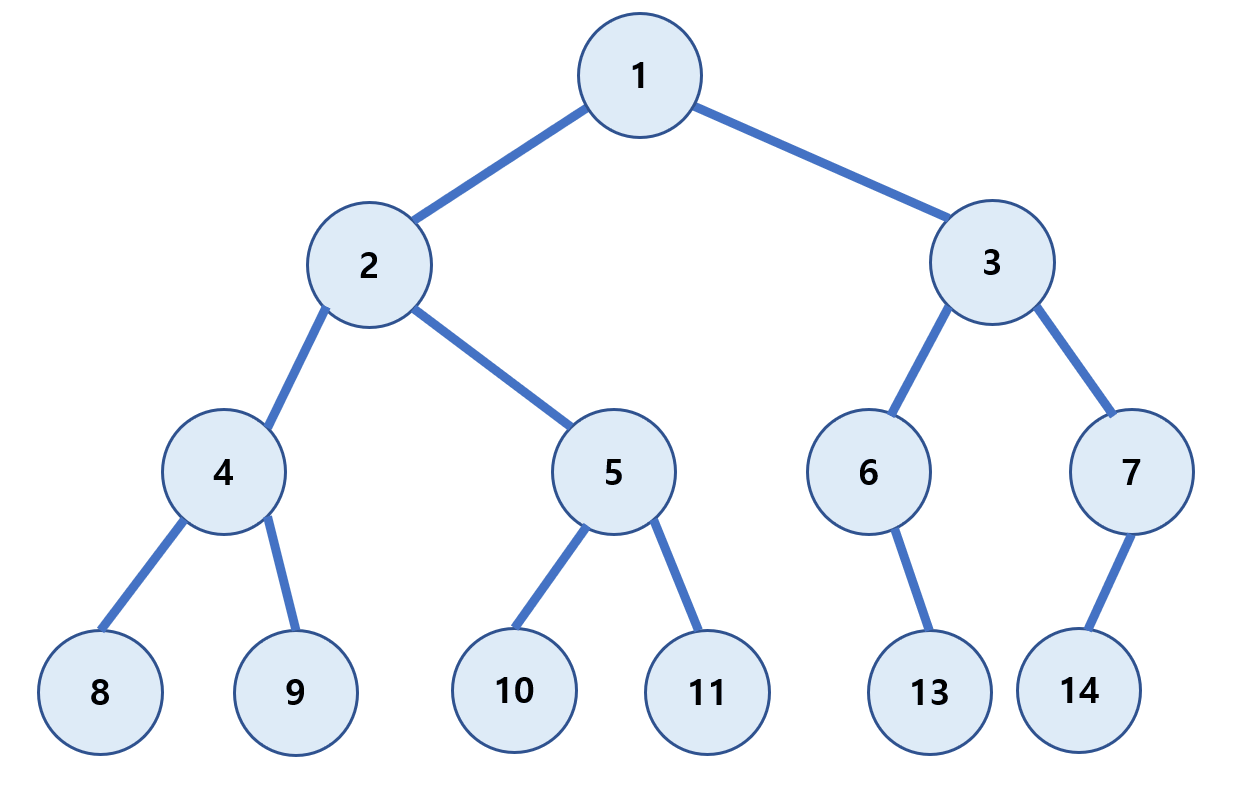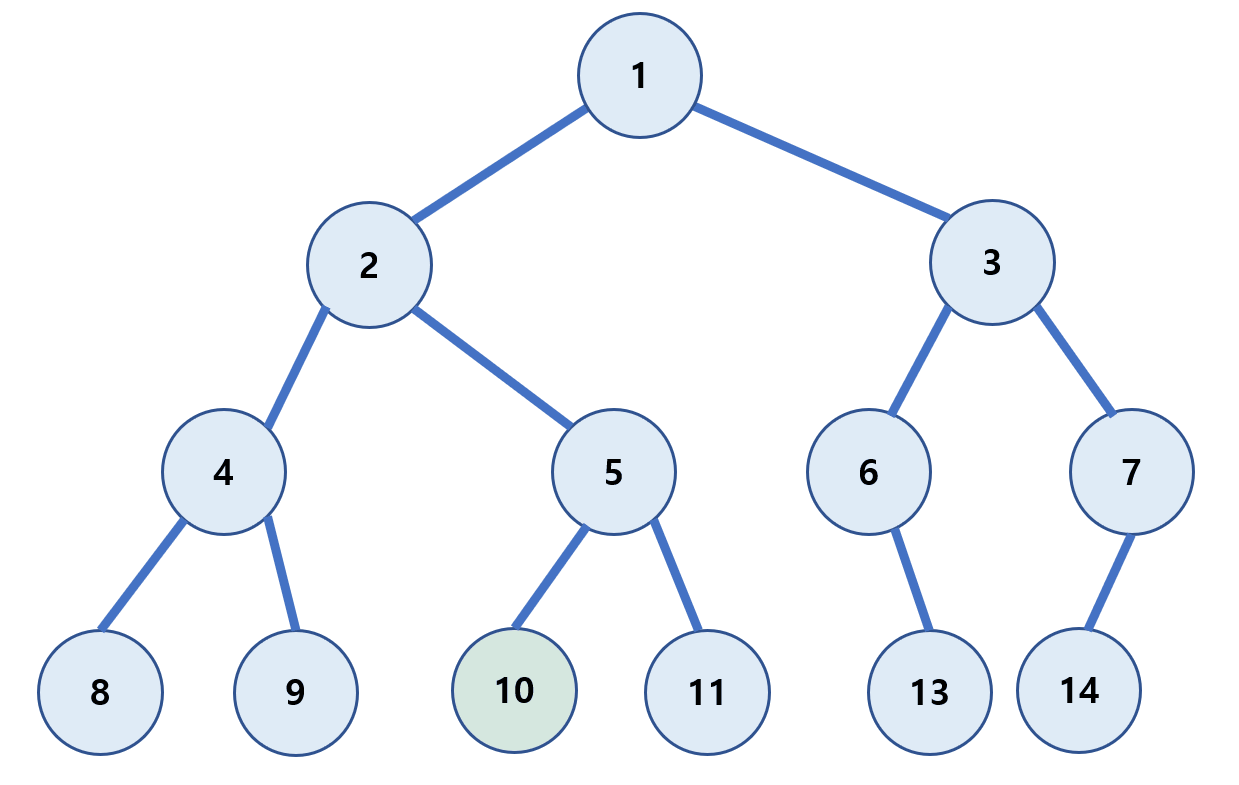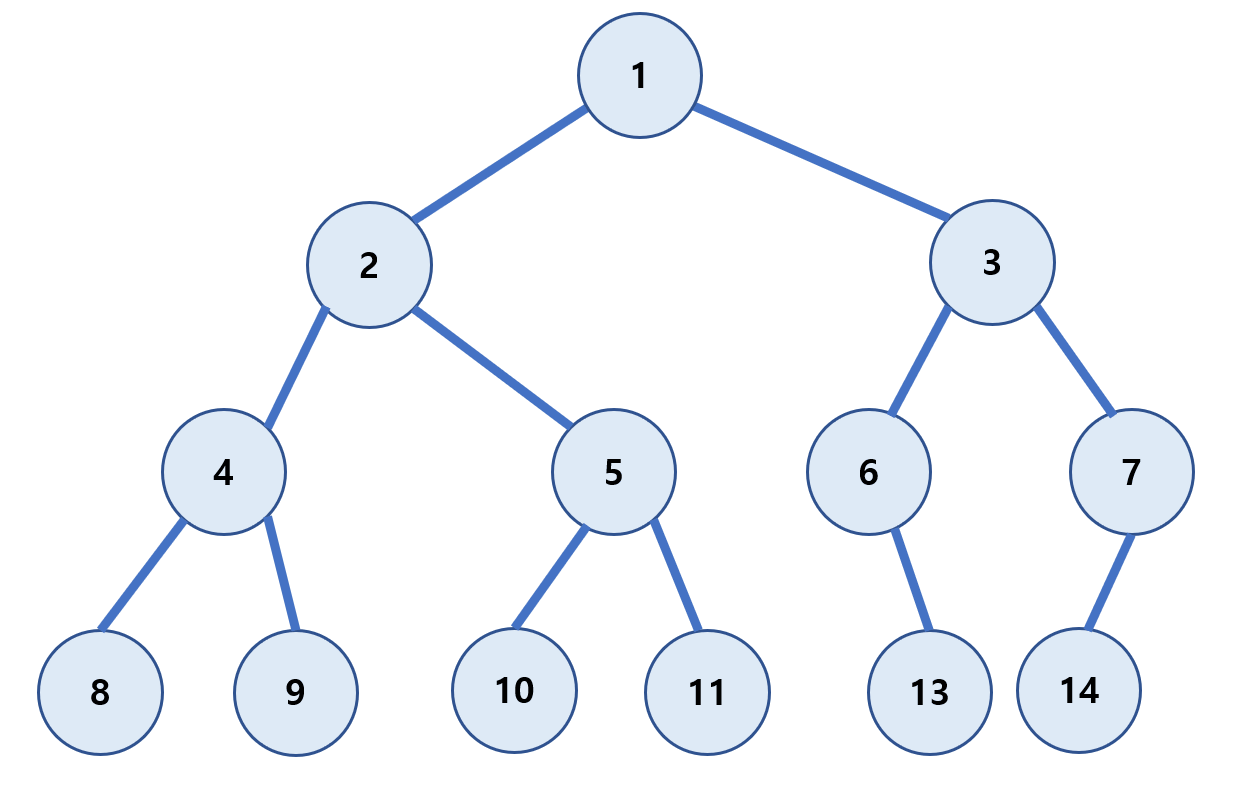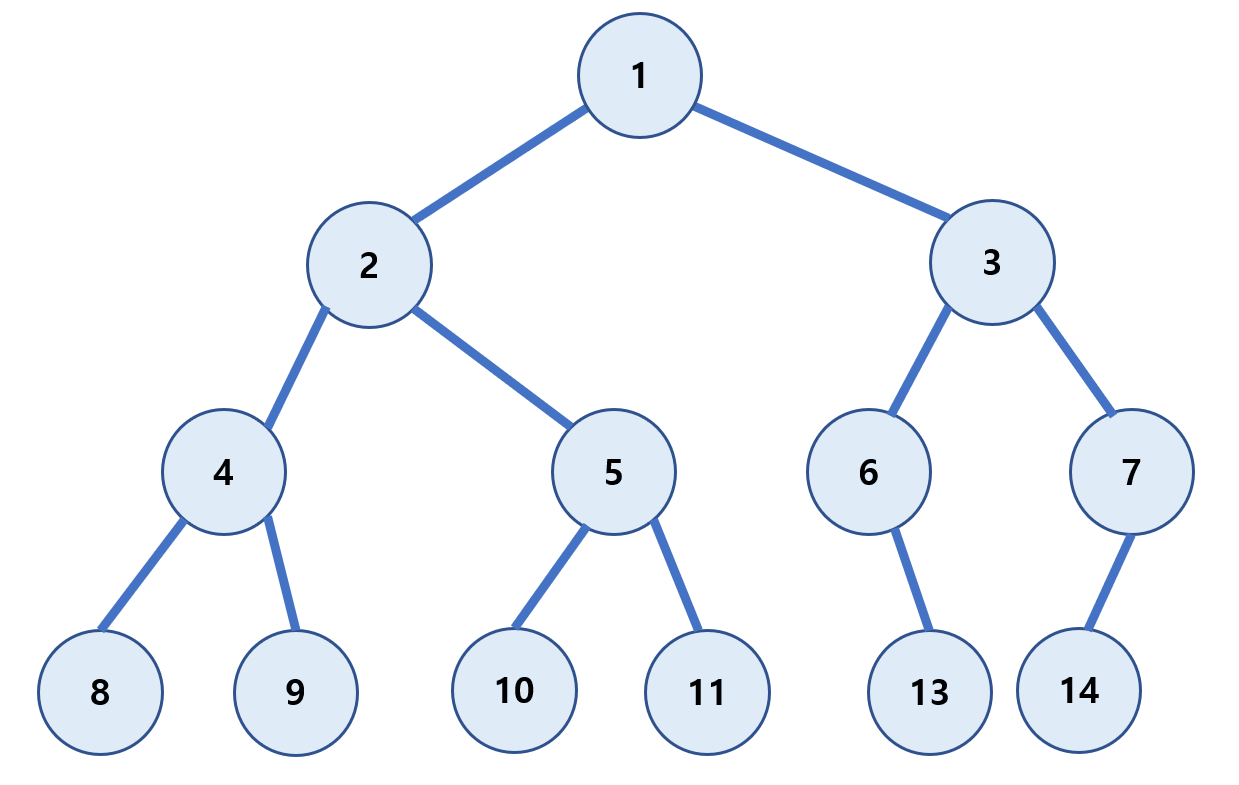
8 → 4 → 9 → 2 → 10 → 5 → 11 → 1 → 6 → 13 → 3 →14 → 7
후위 순회(post-order)
왼쪽 하위 트리부터 하위를 모두 방문 후 루트(Root)를 방문하는 방식이다.
(왼쪽 자식 → 오른쪽 자식 → Root)
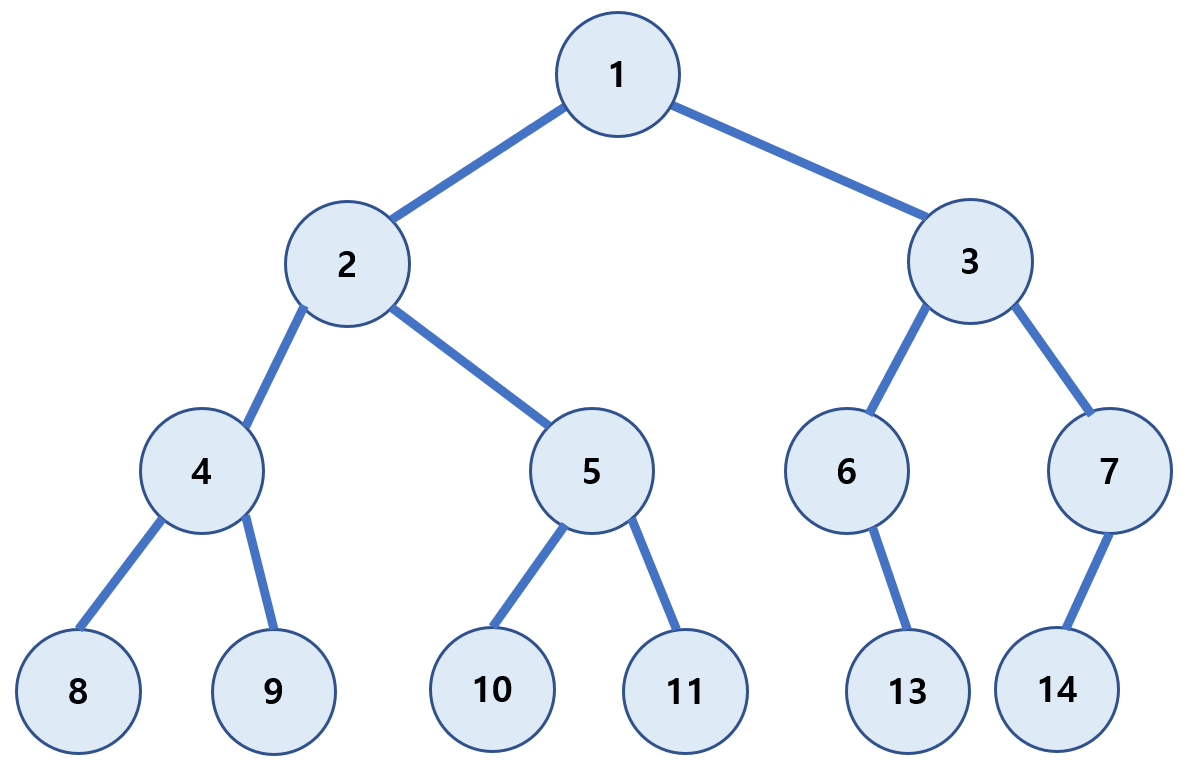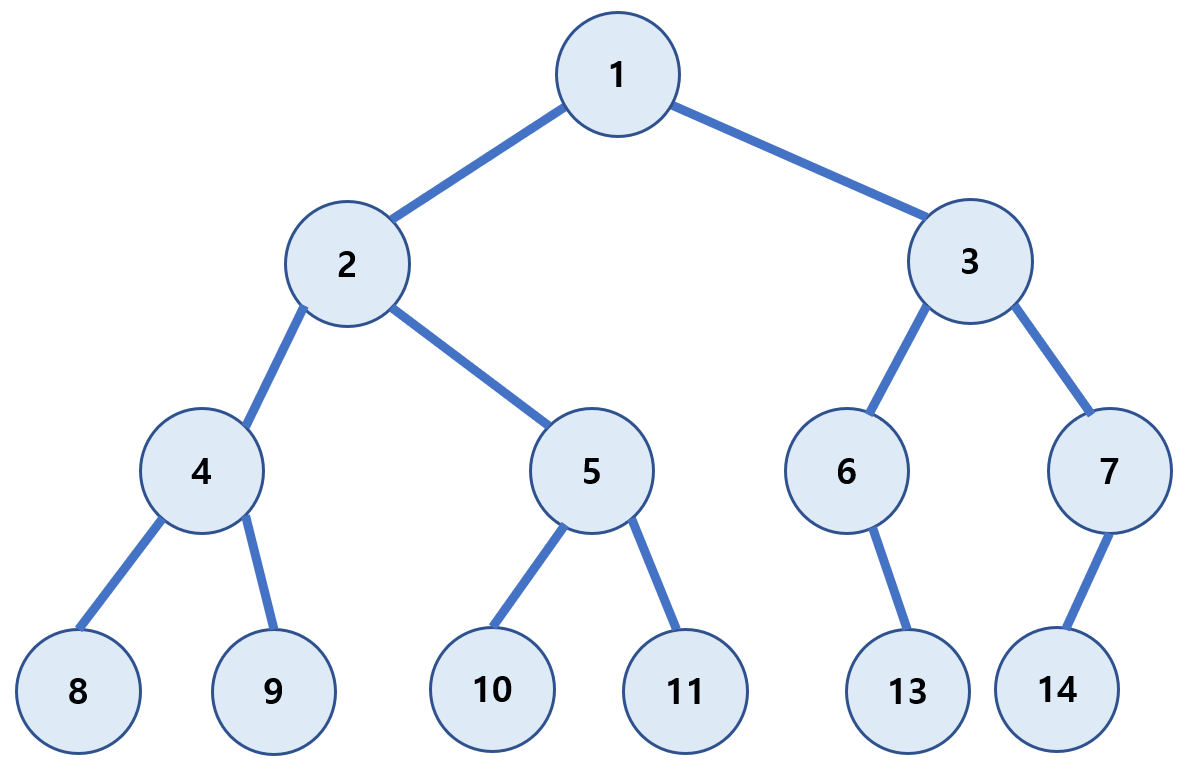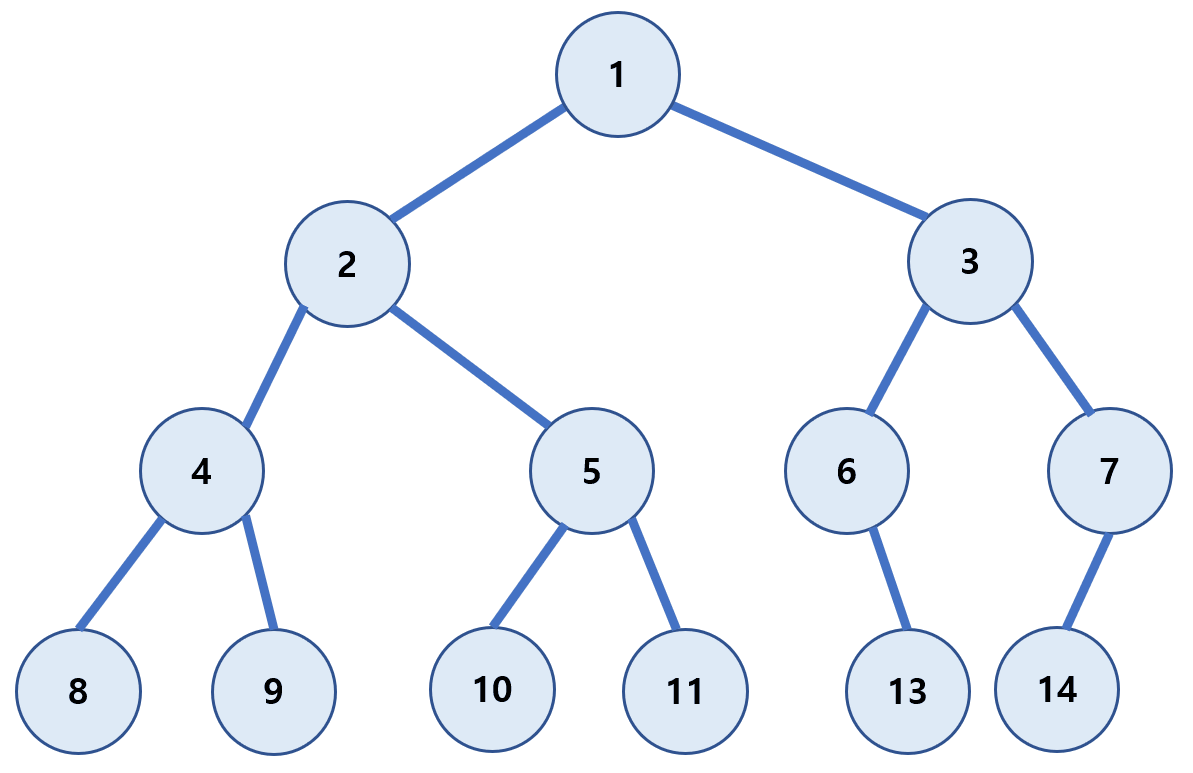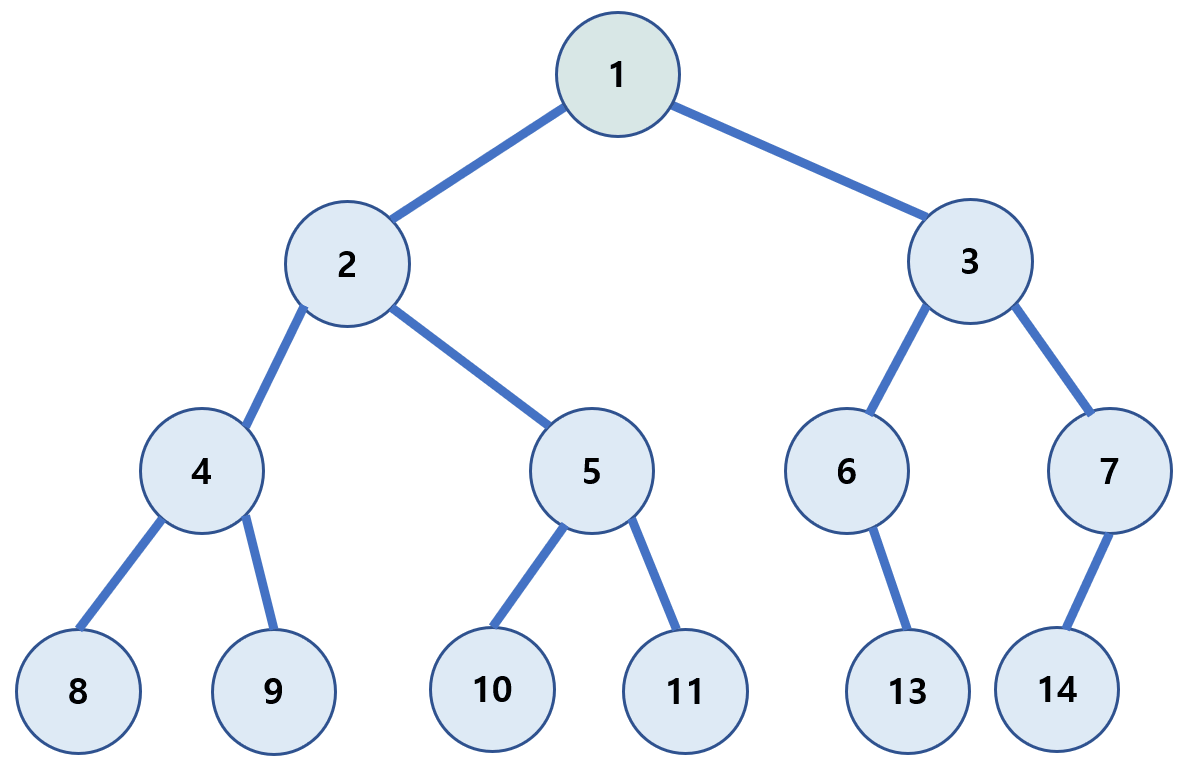
8 → 9 → 4 → 10 → 11 → 5 → 2 → 13 → 6 → 14 → 7 → 3 → 1
레벨 순회(level-order)
루트(Root)부터 계층 별로 방문하는 방식이다.
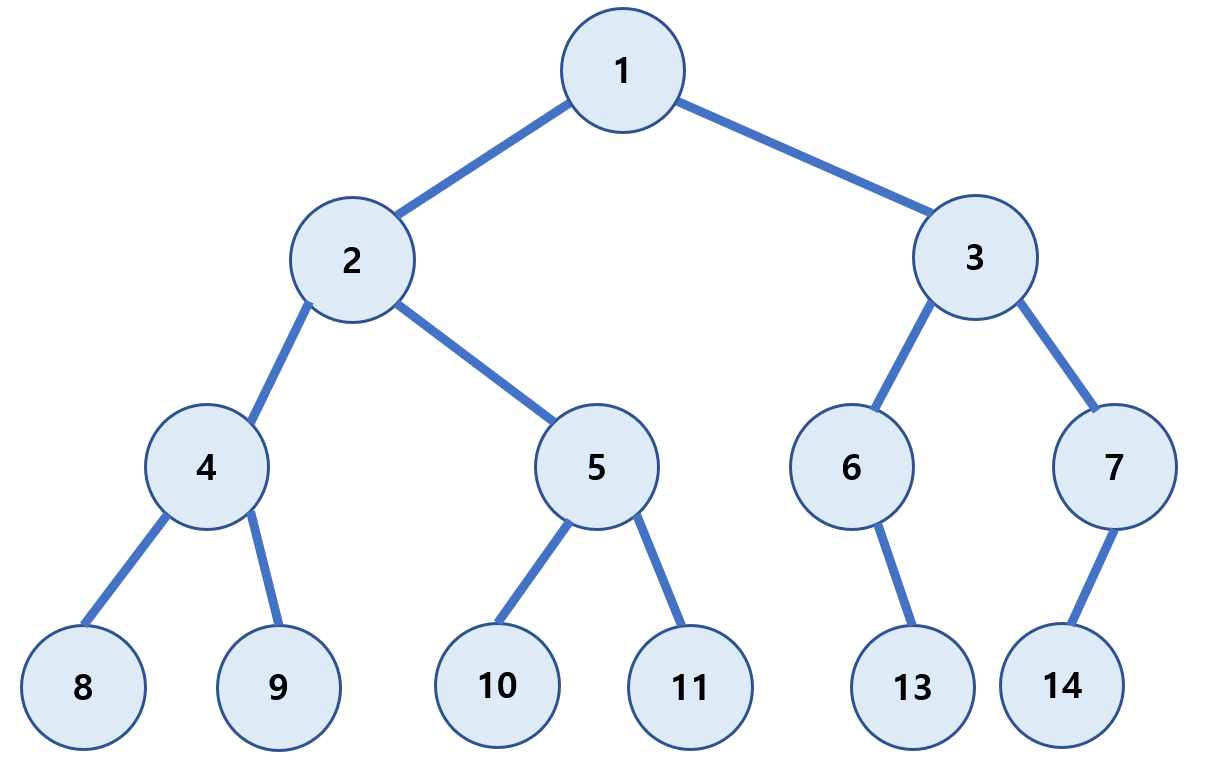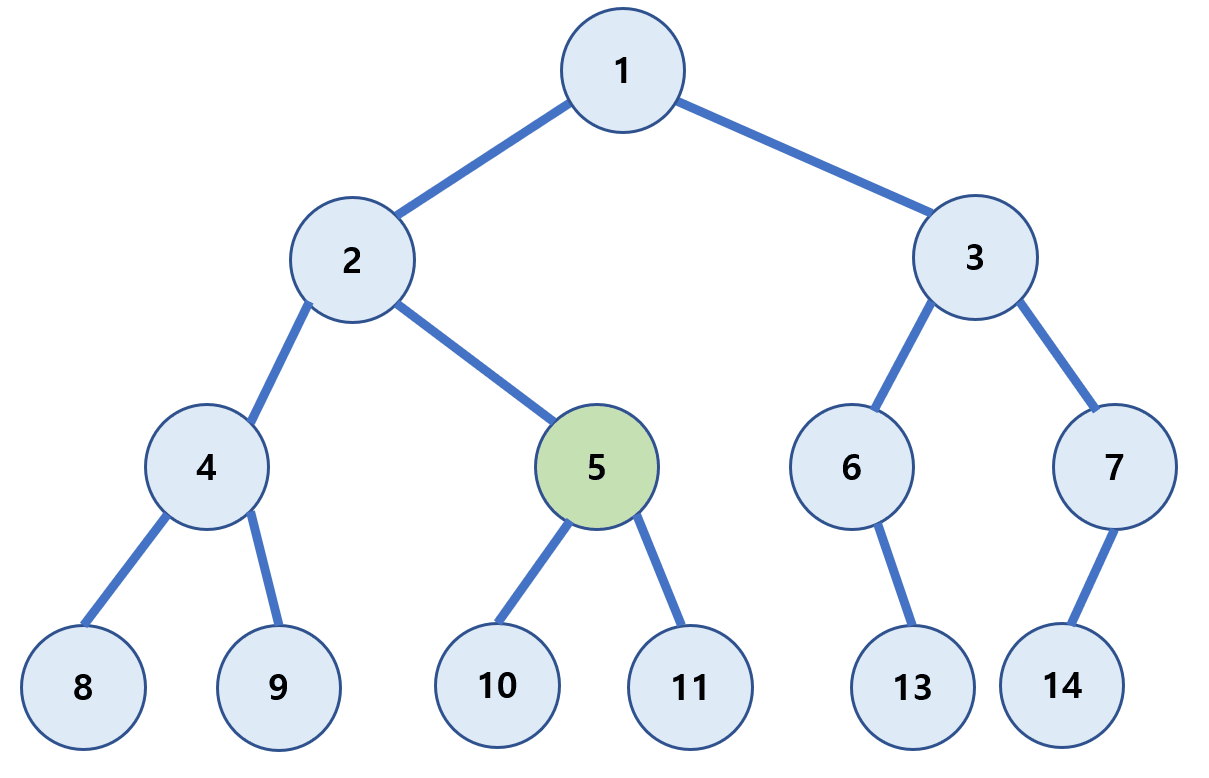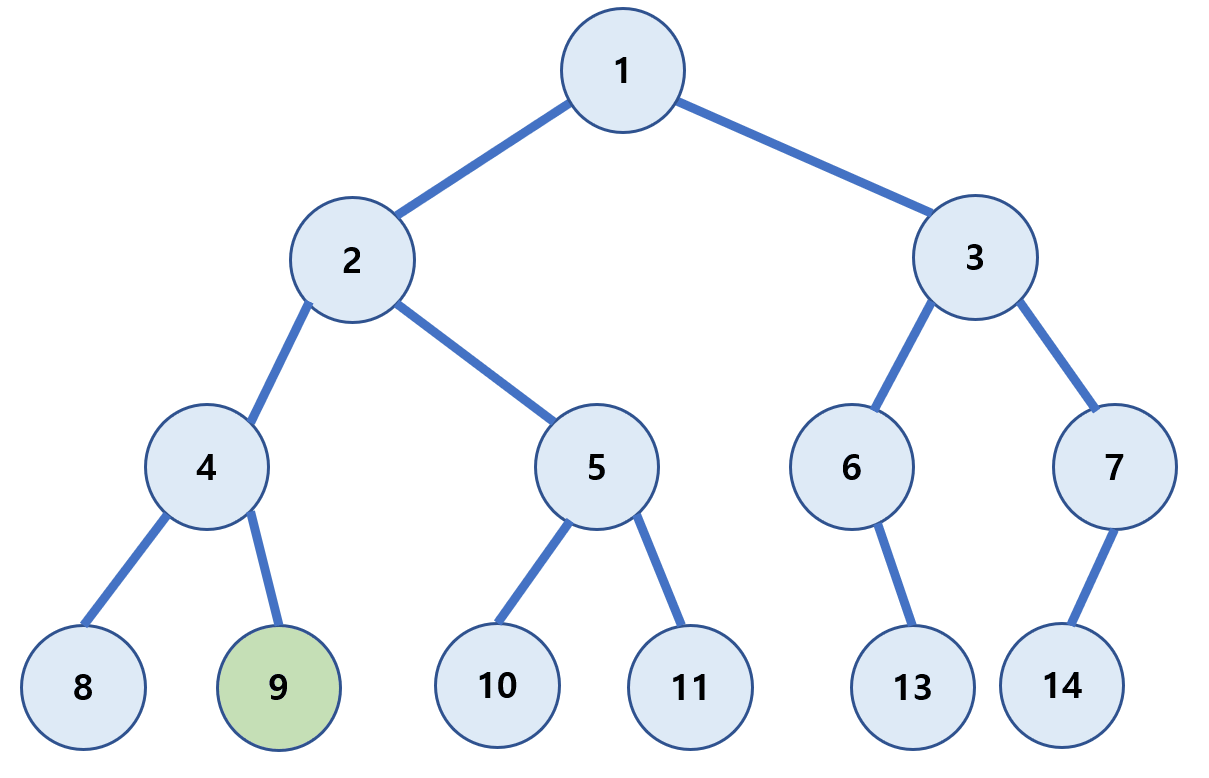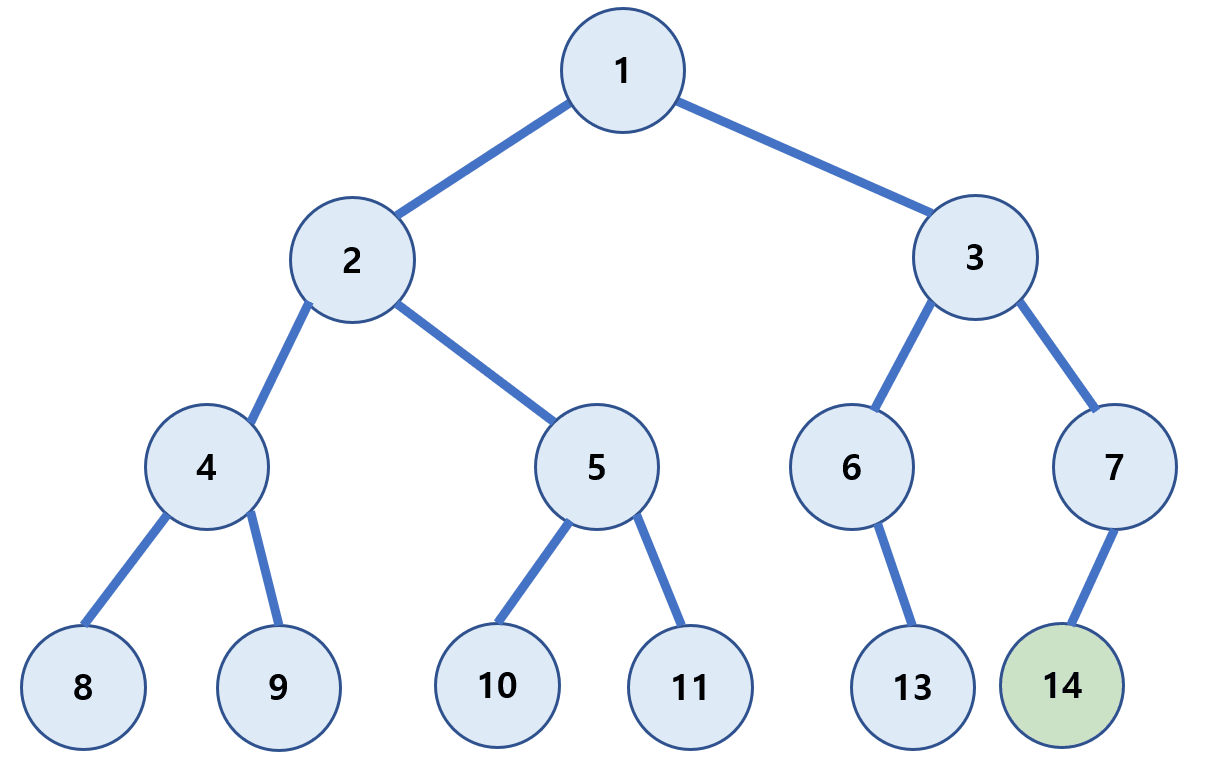
1 → 2 → 3 → 4 → 5 → 6 → 7 → 8 → 9 → 10 → 11 → 13 → 14
코드로 보기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
class Node {
int data;
Node left;
Node right;
}
class Tree {
public Node root;
public void setRoot(Node node) { // 루트 노드
this.root = node;
}
public Node getRoot() {
return root;
}
public Node createNode(Node left, int data, Node right) {
Node node = new Node();
node.data = data;
node.left = left;
node.right = right;
return node;
}
// 중위 순회 Inorder = Left -> Root -> Right
public void inOrder(Node node) {
if(node != null) {
inOrder(node.left); // left
System.out.print(node.data + " → "); // 루트
inOrder(node.right); // right
}
}
// 전위순회 Preorder = Root -> Left -> Right
public void preOrder(Node node) {
if(node != null) {
System.out.print(node.data + " → "); // root
preOrder(node.left); // left
preOrder(node.right); // right
}
}
//후위순회 Postorder = Left -> Right -> Root
public void postOrder(Node node) {
if(node != null) {
postOrder(node.left); // left
postOrder(node.right); // right
System.out.print(node.data + " → "); // root
}
}
}
public class Main {
public static void main(String[] args) {
Tree t = new Tree();
Node n14 = t.createNode(null, 14, null);
Node n13 = t.createNode(null, 13, null);
Node n9 = t.createNode(null, 9, null);
Node n8 = t.createNode(null, 8, null);
Node n7 = t.createNode(n14, 7, null);
Node n6 = t.createNode(null, 6, n13);
Node n11 = t.createNode(null, 11, null);
Node n10 = t.createNode(null, 10, null);
Node n4 = t.createNode(n8, 4, n9);
Node n5 = t.createNode(n10, 5, n11);
Node n2 = t.createNode(n4, 2, n5);
Node n3 = t.createNode(n6, 3, n7);
Node n1 = t.createNode(n2, 1, n3);
t.setRoot(n1); // 루트 노드
System.out.println("전위 순회");
t.preOrder(t.getRoot());
System.out.println();
System.out.println("중위 순회");
t.inOrder(t.getRoot());
System.out.println();
System.out.println("후위 순회");
t.postOrder(t.getRoot());
}
}

출처
Tree
자바 [JAVA] - Binary Search Tree (이진 탐색 트리) 구현하기
[자료구조] 트리(Tree)의 개념 | 이진 트리, 전 이진 트리, 완전 이진트리, 포화 이진 트리, 이진 탐색트리