Stack

Stack

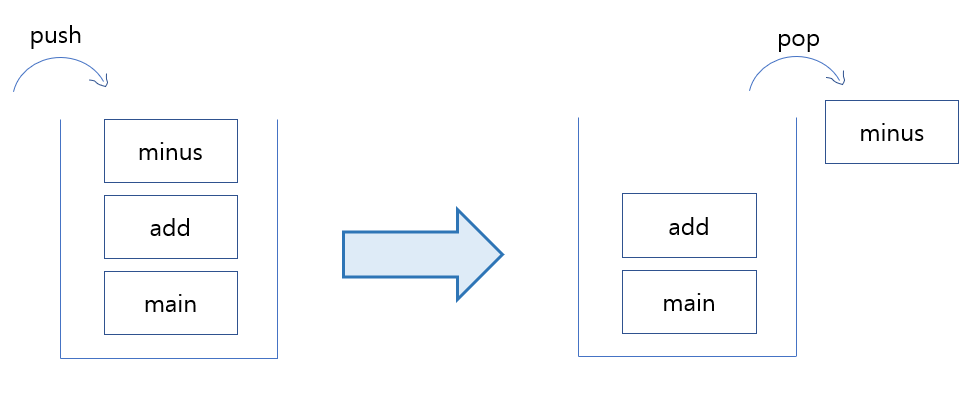
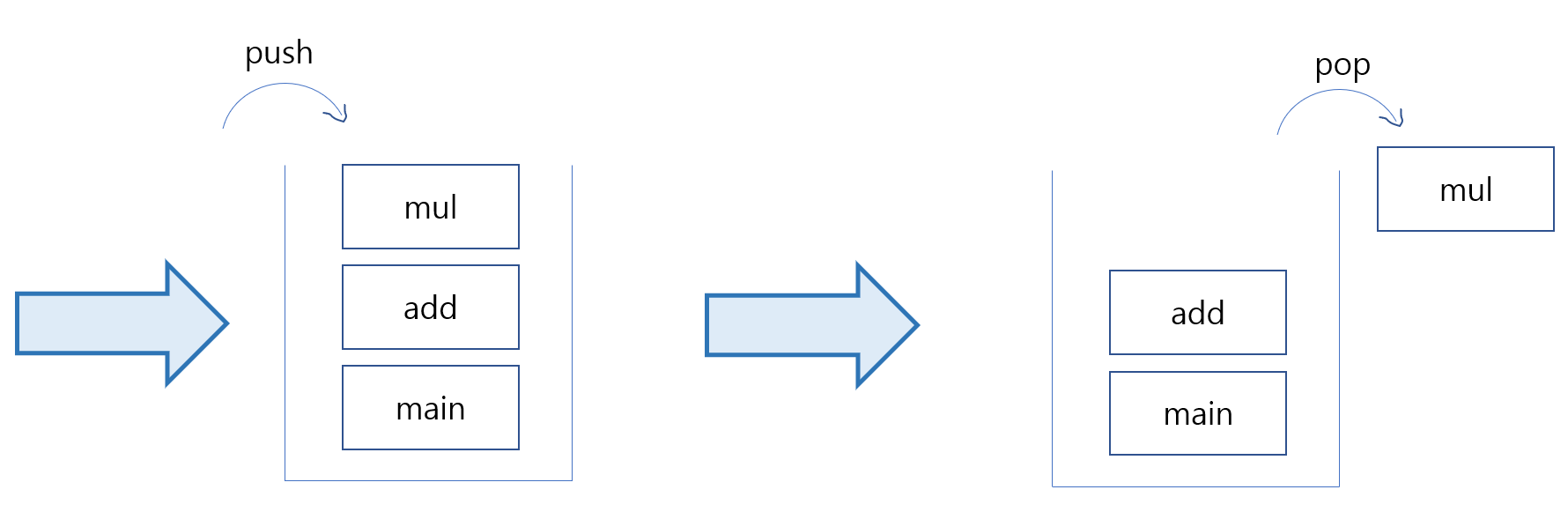
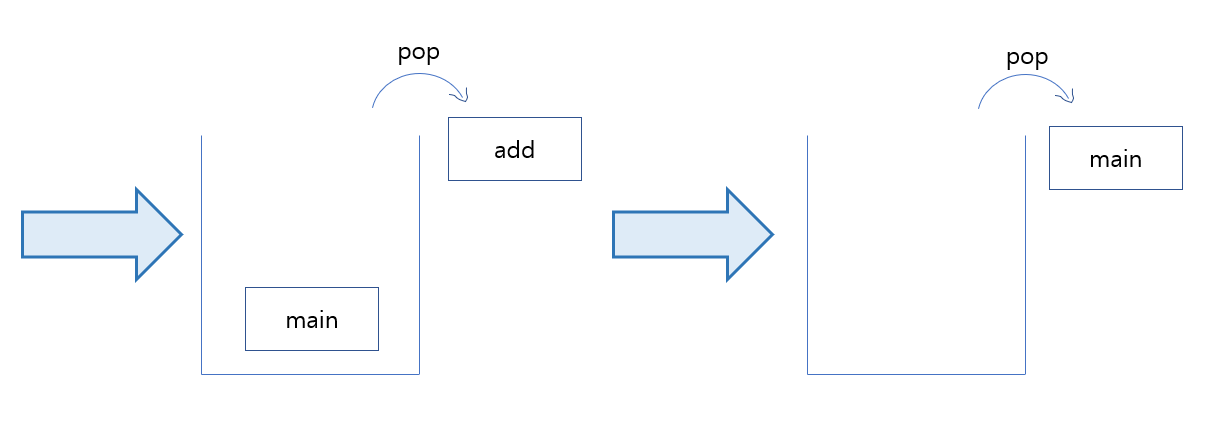
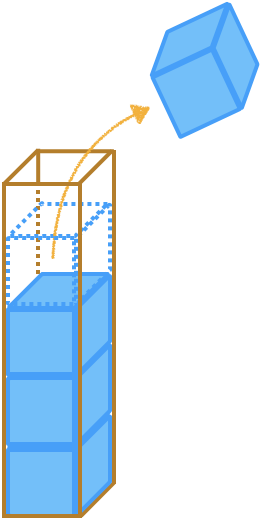
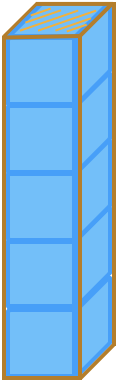
가장 마지막으로 들어간 데이터가 가장 첫 번째로 나오는 성질(LIFO(후입선출), Last In First Out)을 가진 자료 구조이다.

JVM

public class JvmStack {

    public static void main(String[] args) {
        JvmStack jvmStack = new JvmStack();
        jvmStack.add();
    }

    public void add(){
        minus();
        mul();
    }

    public void minus(){
        System.out.println("minus");
    }
    public void mul(){
        System.out.println("mul");
    }
}

특징

• 배열과 달리 index 같은 위치 값으로 접근할 수가 없다.
  검색시. 제일 상위 값부터 검색해야 하므로 O(1)~O(n) 의 시간이 걸린다.
• 데이터 추가 및 삭제는 O(1)
  배열처럼 원소들을 하나씩 밀어줄 필요가 없다.
• 한 쪽 끝에서만 자료를 넣고 뺄 수 있다.
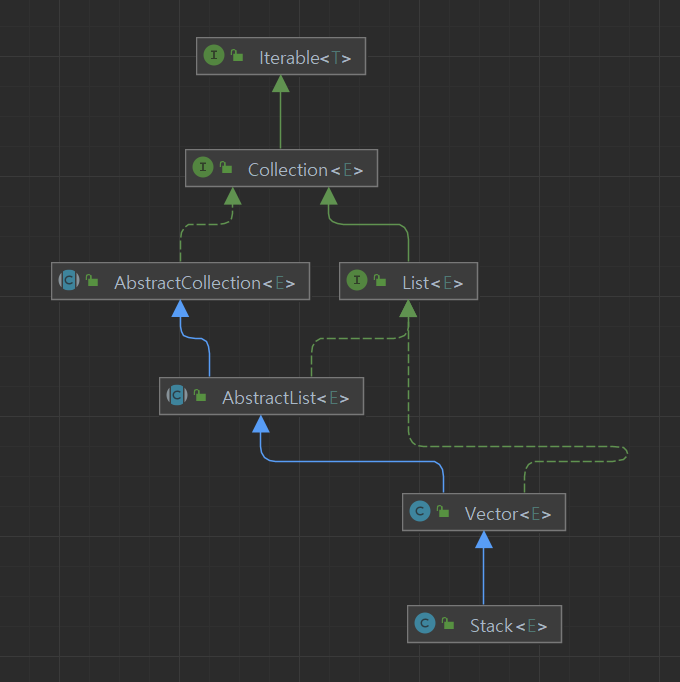
• Stack이 List도 상속받고 있어 List의 메소드도 사용가능하다.

기본연산

• pop() : 스택에서 가장 위에 있는 항목을 제거한다.
• push(item) : item 하나를 스택의 가장 윗 부분에 추가한다.
• peek() : 스택의 가장 위에 있는 항목을 반환(조회)한다. pop 메소드와는 달리 스택에서 제거하지는 않는다.
• isEmpty() : 스택이 비어 있을 때에 true를 반환한다.
• clear() : 스택에 존재하는 모든 자료들을 삭제한다.

push와 pop할 때는 해당 위치를 알고 있어야 하므로 기억하고 있는 ‘스택 포인터(SP)’가 필요하다.

스택 포인터는 다음 값이 들어갈 위치를 가리키고 있다. (처음 기본값은 -1)

public boolean isEmpty(){
    return sp == -1;
}

push()

item 하나를 스택의 가장 윗 부분에 추가

pop()

스택에서 가장 위에 있는 항목을 제거

peek()

스택의 가장 위에 있는 항목을 반환

isEmpty()

스택이 비어 있을 때에 true를 반환

isFull()

스택이 꽉차 있을 때 true를 반환

동작 배열 스택

스택에는 MAX_SIZE라는 최대 크기가 존재해야 한다.

→ 스택 포인터와 MAX_SIZE를 비교해서 isFull 메소드로 비교해야되기 때문이다.

최대 크기가 없는 스택을 만드려면?

arraycopy를 활용한 동적배열 사용한다.(스택이 최대가 되면 스택 크기를 2배로 늘리는 방법이다.)

활용

• 재귀 알고리즘
• 웹 브라우저 방문기록(뒤로가기)
• 실행 취소
• 역순 문자열 만들기
• 수식의 괄호 검사
• 후위 표기법 계산