이진 탐색 트리(Binary Search Tree)
Binary Search Tree → Binary(이진), Search(탐색), Tree(트리) : 이분화된 탐색을 위한(혹은 특화된) 트리 자료구조
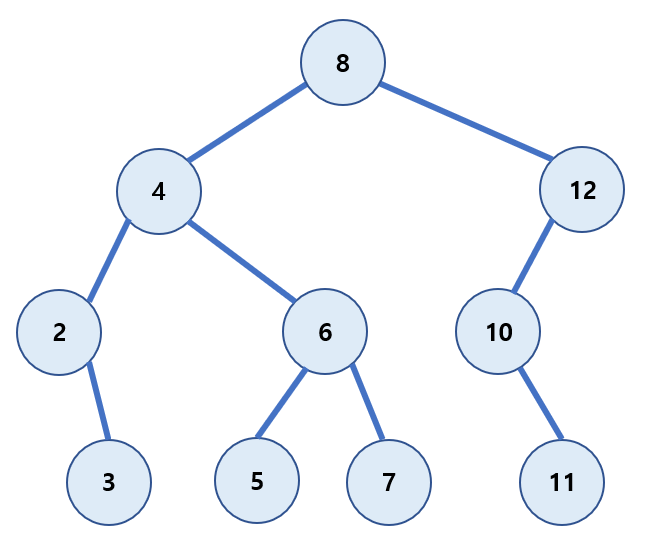
이진
Binary(이진) → 이분화 된다.
트리 구조에서 특정한 형태로 제한을 하게 되는데, 모든 노드의 최대 차수를 2로 제한한 것이다.
→ 각 노드는 자식노드를 최대 2개까지밖에 못갖는다.
이를 ‘이진 트리(Binary Tree)‘라고 한다.
탐색에 특화된 트리
“부모 노드를 기준으로 왼쪽 자식 노드들은 부모 노드보다 값이 작으며, 오른쪽 자식 노드들은 부모 노드보다 값이 크다.”
이렇게 구성하면 이진 탐색 트리가 되는 것이다.
목적
이진탐색 + 연결리스트
이진탐색 : 탐색에 소요되는 시간복잡도는 O(logN), but 삽입,삭제가 불가능
연결리스트 : 삽입, 삭제의 시간복잡도는 O(1), but 탐색하는 시간복잡도가 O(N)
이 두가지를 합하여 장점을 모두 얻는 것이 `이진탐색트리’다.
즉, 효율적인 탐색 능력을 가지고, 자료의 삽입 삭제도 가능하게 만든다.
특징
- 각 노드의 자식이 2개 이하
- 각 노드의 왼쪽 자식은 부모보다 작고, 오른쪽 자식은 부모보다 크다.
- 중복된 노드가 없어야 한다.
굳이 중복을 한다고 하면 왼쪽 노드 조건을 부모랑 같거나 작은으로 바꿀 수도 있고,
혹은 오른쪽 노드 조건을 부모랑 같거나 큰으로 바꾸면 된다. (단, 양쪽 노드 모두 같을경우를 적용하면 안된다)
중복이 없어야 하는 이유?
검색 목적 자료구조인데, 굳이 중복이 많은 경우에 트리를 사용하여 검색 속도를 느리게 할 필요가 없다.
(트리에 삽입하는 것보다, 노드에 count 값을 가지게 하여 처리하는 것이 훨씬 효율적이다.)
이진탐색트리의 순회는 ‘중위순회(inorder)’ 방식 (왼쪽 - 루트 - 오른쪽)
중위 순회로 정렬된 순서를 읽을 수 있다.
핵심 연산
- 검색
- 삽입
- 삭제
- 트리 생성
- 트리 삭제
시간 복잡도
- 균등 트리 : 노드 개수가 N개일 때
O(logN) - 편향 트리 : 노드 개수가 N개일 때
O(N)
삽입, 검색, 삭제 시간복잡도는 트리의 Depth에 비례한다.
삽입
새로운 노드가 위치할 곳을 탐색하는 과정이 필요하다.
1-1. 루트 노드에 값이 없는 경우는 트리가 없는 경우이므로 루트에 넣는다.
1-2. 루트에 값이 있고 삽입되는 값이 루트보다 작으면 왼쪽으로 탐색시킨다.
1-3. 루트에 값이 있고 삽입되는 값이 루트보다 크면 오른쪽으로 탐색시킨다.
2. 해당 방향으로 탐색을 진행했을 때, 탐색 위치에 값이 없으면 해당 위치에 노드를 추가한다.
삭제
삭제하려는 노드가 단말 노드인 경우
삭제하려는 노드가 한쪽 자식 노드만 가지는 경우
삭제하려는 노드가 모든 자식 노드를 가지는 경우
삭제하려는 노드가 단말 노드인 경우
삭제하는 노드가 자식노드를 갖고 있지 않을 때 해당 노드만 삭제해주면 된다.
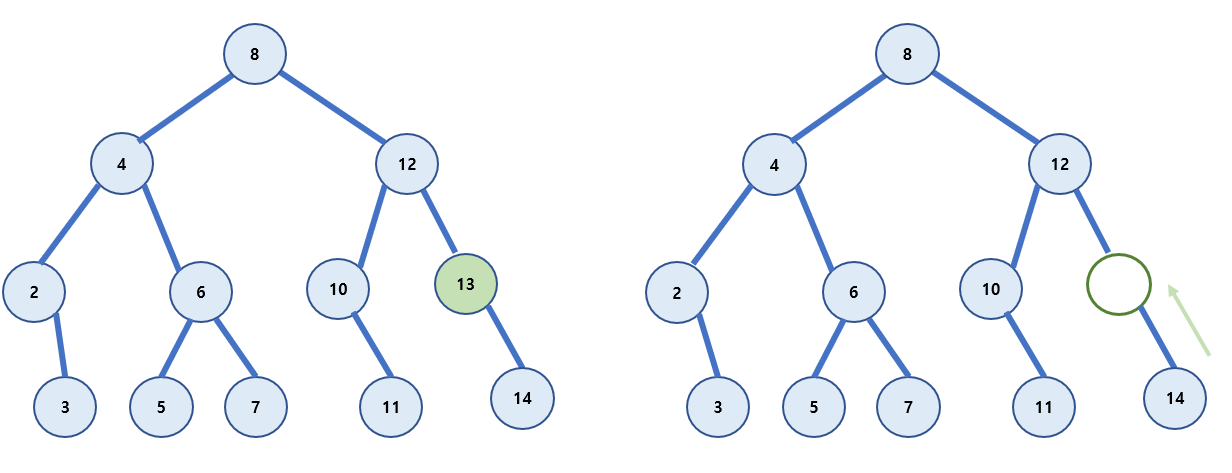
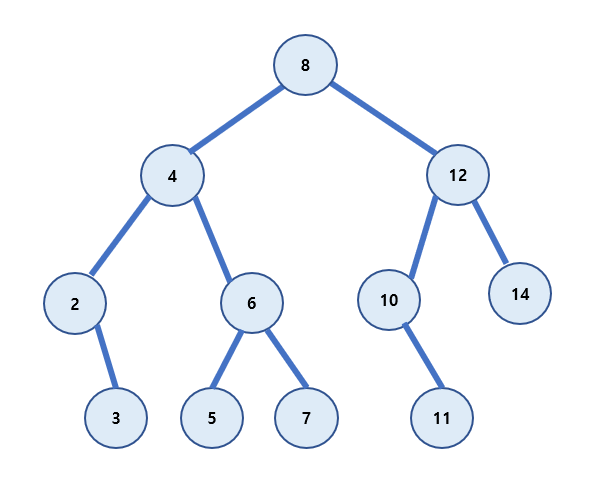
삭제하려는 노드가 한쪽 자식 노드만 가지는 경우
삭제하는 노드가 왼쪽 또는 오른쪽 자식 노드를 갖고 있을 때 자식노드를 삭제노드의 위치로 옮겨오면 된다.
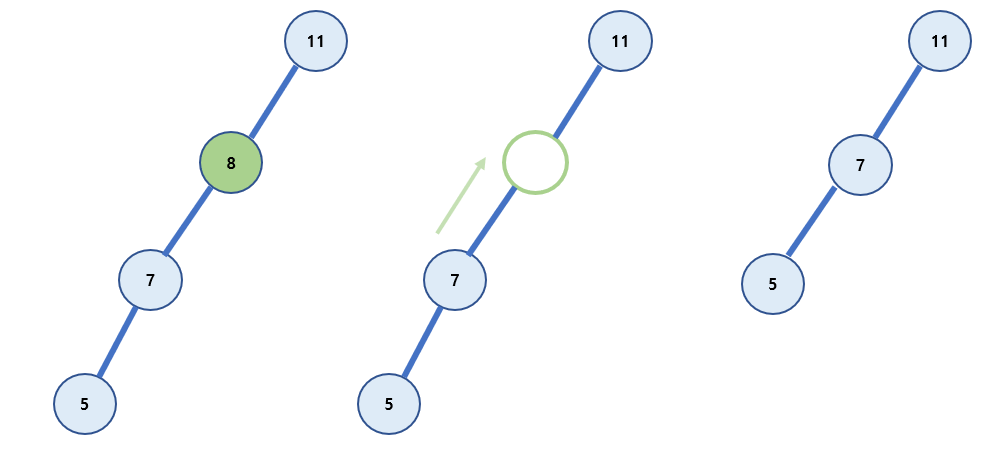
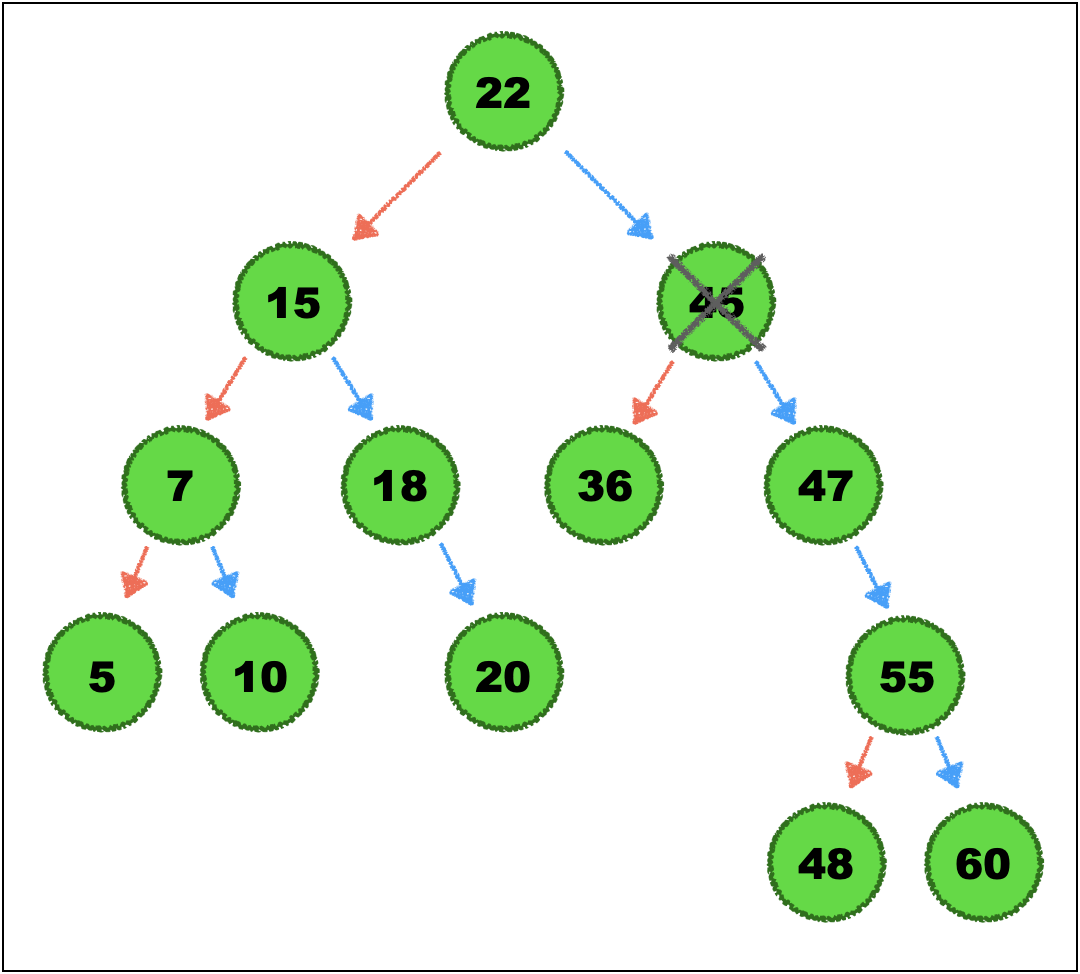
삭제하려는 노드가 모든 자식 노드를 가지는 경우
삭제하는 노드가 왼쪽, 오른쪽 자식 노드 모두 갖고 있을 때
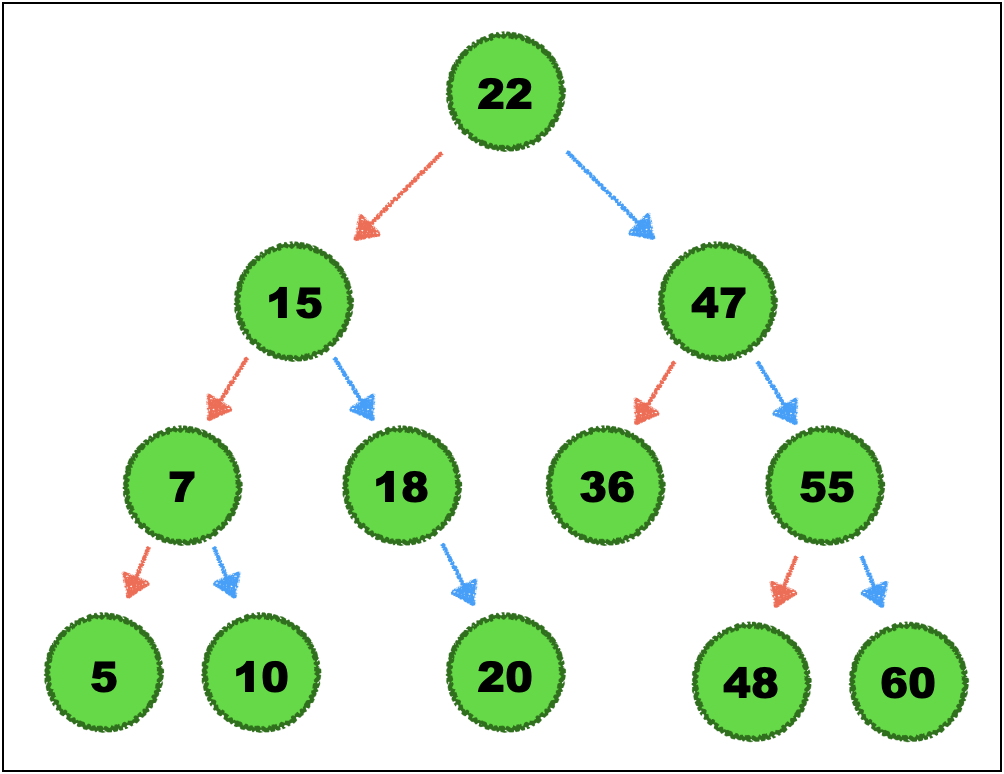
방법 1. 삭제된 노드의 오른쪽 자식 노드에서 제일 작은 노드로 대체하는 방법
방법 2. 삭제된 노드의 왼쪽 자식 노드에서 제일 큰 노드로 대체하는 방법
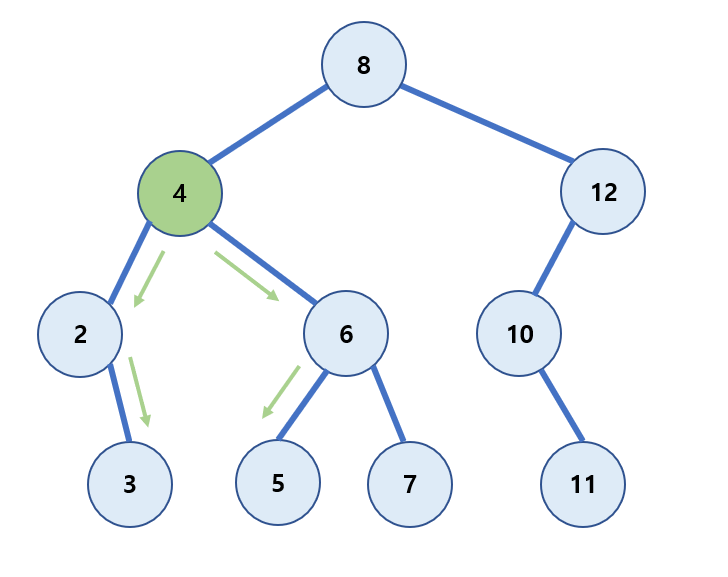
🐣 삭제 노드의 오른쪽 노드는 무조건 왼쪽 노드를 타야하고 삭제 노드의 왼쪽 노드는 무조건 오른쪽 노드를 타야한다.
탐색
- 전위 탐색 :
Root, 왼쪽 자식 노드, 오른쪽 자식 노드 순서로 방문한다. - 후위 탐색 : 왼쪽 자식 노드, 오른쪽 자식 노드,
Root순서로 방문한다. - 중위 탐색 : 왼쪽 자식 노드,
Root, 오른쪽 자식노드 순서로 방문한다.
출처
이진 탐색 트리: 이론과 소개
이진 탐색 트리: 자바 언어로 구현하기
이진탐색트리 (Binary Search Tree)
자바 [JAVA] - Binary Search Tree (이진 탐색 트리) 구현하기
읽으면 좋은 링크
이진탐색트리(Binary Search Tree)
CH8. 트리(Tree) 3 (이진 트리의 순회 (Traversal))