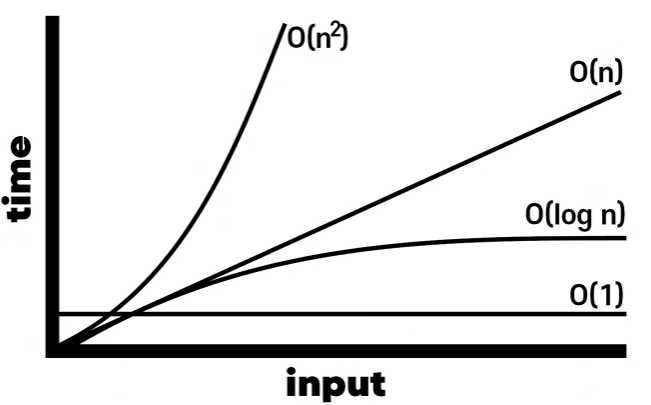
Big o

Big O

참고로 아래 영상을 보면서 정리한 글이다.
개발자라면 이제는 알아야하는 Big O 설명해드림. 10분컷.

알고리즘 스피드의 표현법

같은 알고리즘 이라도 컴퓨터라는 하드 웨어에 따라서 컴퓨터 마다 속도가 다를 수 있다.

그렇기 때문에 “빠르다”, “느리다” 라는 “시간”으로 표현하지 않는다.

👉🏻 알고리즘 스피드는 “완료까지 걸리는 절차의 수”로 결정 된다.

Linear Search(선형 검색)

선형 검색은 한 개씩 검색을 한다. 데이터가 10개면 해당 값을 찾기 까지 10개 스텝이 필요하다.

→ input size = N 이라면 선형 알고리즘은 N steps 가 요구된다.

→ 선형 검색의 시간 복잡도는 O(n)을 갖는다.

이렇듯 Big O를 사용하면 시간 복잡도를 빠르게 설명할 수 있다.

O(1) : constant time

input size에 관계 없이 step이 정해진 알고리즘

public class BigO {
    String[] arr = {"hae", "dal", "coco", "lulu", "hihi", "lala", "inging"};

    public void printFirst() {
        System.out.println(arr[0]); // 배열의 첫 번째 요소 출력
    }


    public static void main(String[] args) {
        BigO bigO = new BigO();
        bigO.printFirst();
    }
}

input size = 7이고 해당 함수는 1번이면 실행이 끝난다.

input size가 100개가 된다 해도 끝내는 것은 1번이면 된다.

→ input이 얼마나 큰지 작은지에 관계 없이 해당 함수는 동일한 수의 스텝이 필요하다.

→ 이 함수의 시간 복잡도는 constant time (상수시간) 이라고 할 수 있다.

N이 크기에 관계 없이 끝내는데 동일한 숫자의 스텝이 필요하다.

이것을 Big O로 표현하면 O(1)이다.

만약 출력을 2번 하면 2개의 스텝이 필요하므로 시간 복잡도는 O(2)가 될까?

public void printFirst() {
    System.out.println(arr[0]);
    System.out.println(arr[0]);
}

답은 ❌로 시간 복잡도는 O(1)이다.

Big O는 함수의 디테일에 신경을 쓰지 않고 input size에 따라 어떻게 이 함수가 작동하는지를 본다.

해당 함수는 input size에 관계없이 정해진 숫자에 따라 작동한다.

따라서 출력을 여러 번 시켜도 O(1)이 된다.

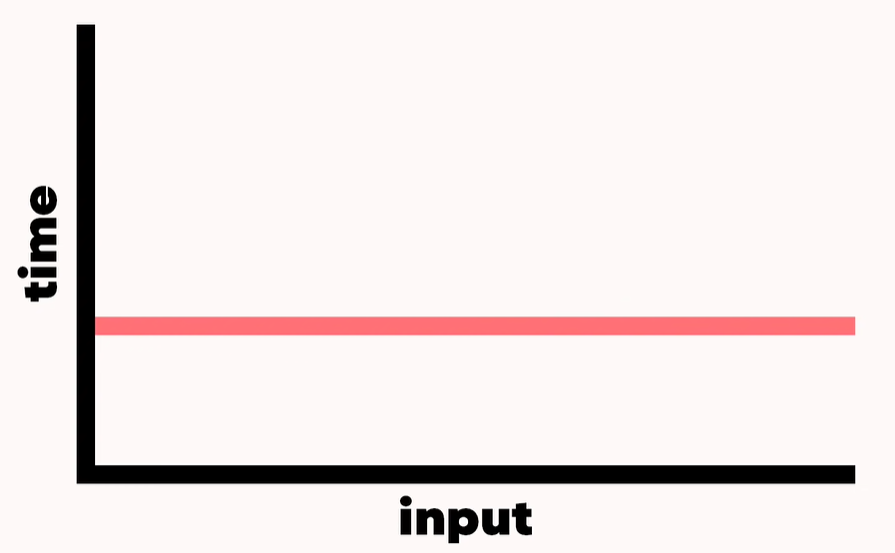
🐣 Big O는 상수(constant)에 신경을 쓰지 않는다!

O(N)

public class BigO {
    String[] arr = {"hae", "dal", "coco", "lulu", "hihi", "lala", "inging"};

    public void printAll() {
        for(int i=0; i<arr.length; i++) {
            System.out.println(i);
        }
    }


    public static void main(String[] args) {
        BigO bigO = new BigO();
        bigO.printAll();
    }
}

이번에는 각 값들을 모두 출력시키는 함수다. → 배열 사이즈가 7이라면 7번 출력 시킨다.

만약 배열이 N개라면 N개 스텝으로 나올 것이다. (input이 증가하면 step도 증가한다.)

이를 Big O로 표현하면 O(N)이다.

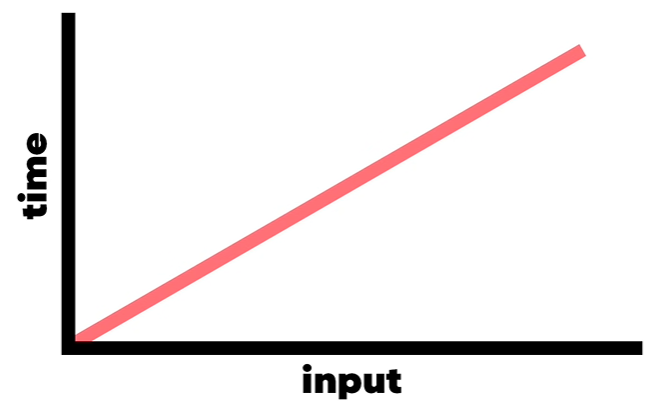
🐣 함수를 반복해도 O(2N)이 아니라 O(N)이다. (상수는 버린다.)

O(n^2)

루프 안의 루프안에서 함수를 실행시켰다.

public void printAll() {
    for(int i=0; i<arr.length; i++) {
        for(int j=0; j<arr.length; j++) {
            System.out.printf("%d, %d", i, j);
        }
    }
}

배열의 각 값에 대해 루프를 반복하여 실행

input이 7개 라면 완성하는데 49번의 스텝이 필요하다.

👉🏻 시간 복잡도는 input의 n^2이다.

O(logN) : Logarithmic time(로그 시간)

*로그(logarithm)는 지수(exponent)의 정 반대다.

이진 검색 알고리즘 설명할 때 쓰인다. (이진 검색은 정렬되지 않은 배열에 사용할 수 없다.)

이진 검색은 각 프로세스의 스텝을 매번 절반으로 나눠서 진행하기 때문에 input size가 2배가 되어도 스텝은 1밖에 증가를 안한다.

10 items → 20 items and 3 steps → 4 steps

👉🏻 시간 복잡도는 O(log N)

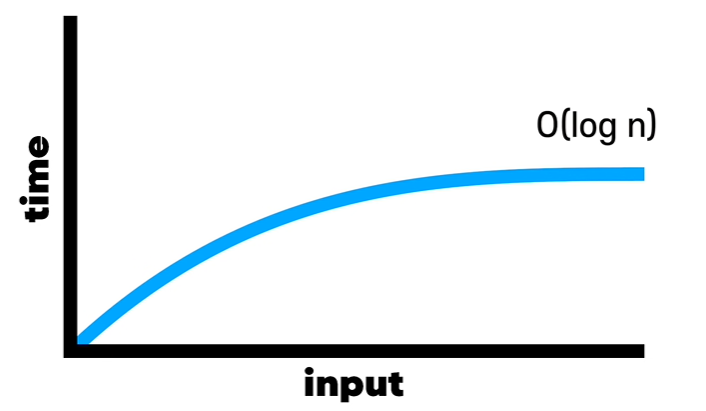
선형 시간보다는 빠르고 상수 시간보다는 느리다.

🐣 Big O에서는 base를 쓰지 않는다.

5 = log2(32)에서 32의 밑이 2인데 Big O의 특성상 및 숫자는 사라진다.

5 = log (32)

정리